Teori Dasar Himpunan Dan Beberapa Referensi Soal

Himpunan ialah sekelompok obyek yang memiliki sifat keterlibatan yang sama dan sanggup dibedakan antara obyek yang satu dengan lainnya. Suatu himpunan biasanya dilambangkan dengan memakai abjad besar, contohnya A,B,C, . . ., sedangkan unsur suatu himpunan dituliskan dengan abjad kecil menyerupai a,b,c,x,y,...

Cara Penulisan Himpunan

Suatu himpunan, sanggup dituliskan dengan dua cara, yaitu :
1. Cara registrasi (Roster Method)
Pada cara ini, unsur himpunan didaftarkan satu persatu, contohnya :
$ A = \left \{ x_{1},x_{2},x_{3},...,x_{n} \right \} $
2. Cara perincian (Rule Method)
Pada cara ini, unsur himpunan dituliskan atas dasar sifat unsur tersebut, umumnya
penulisan pada cara ini ialah $ A = \left \{ x \mid sifat-sifat\ dari\ x \right \} $

Keanggotaan Himpunan

Untuk menyatakan suatu unsur merupakan “anggota“ pada suatu himpunan dipakai lambang “ $ \in $ ” , sedangkan lambang “ $ \notin $ “ dipakai menyatakan “bukan
anggota” dari suatu himpunan.
Contoh :
$ 1.\ A = \left \{ 1, 2, 3 \right \} maka\ 1\in A ; 2\in A ; 3\in A ; 0\notin A ; \left \{1 \right \}\notin A ; 4\notin A.$
$ 2.\ B = \left \{ x \mid x^{2}-x-6=0,\ x\in orisinil \right \}, maka\ 3\in B\ tetapi\ -2\notin B$

Himpunan yang tidak memiliki anggota dinamakan himpunan kosong (empty set) ditulis $ \left \{ \ \right \} $ atau $\varnothing $, contohnya :
$ 1.\ A = \left \{ x \mid x^{2}+5x+6=0,\ x\in orisinil \right \}, maka\ A = \varnothing = \left \{ \ \right \}$

Himpunan Bagian

Definisi: Himpunan A dikatakan himpunan bab dari B jikalau dan hanya jikalau untuk setiap $ x\in A\ maka\ x\in B\ ditulis\ A \subset B$

Sifat :
1. ∅ ⊂ A , A himpunan sembarang
2. A ⊂ B dan B ⊂ C ⇒ A ⊂ C

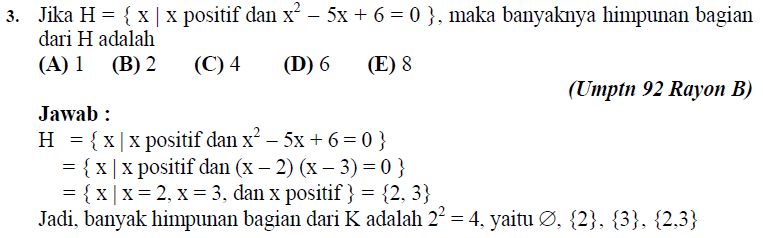
Operasi pada Himpunan

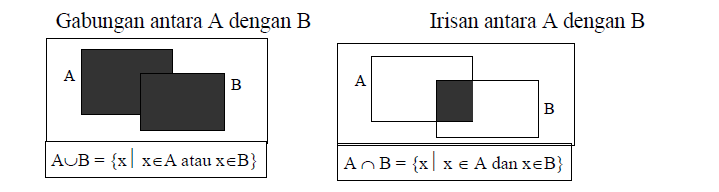
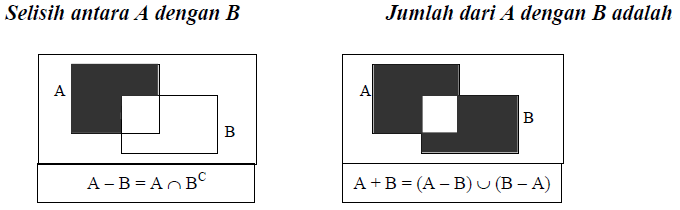
Contoh:

Bilangan Kardinal

Bilangan kardinal dari A ialah bilangan cacah yang menyatakan banyaknya unsur dari A, ditulis n(A).

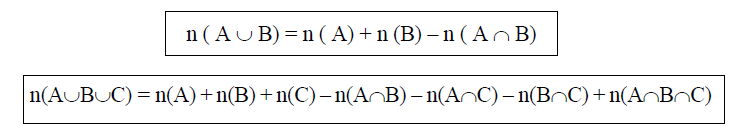
Contoh:









Demikian klarifikasi sederhana wacana teori dasar himpunan dan beberapa teladan soal dan pembahasan yang sudah pernah dikeluarkan dalam seleksi masuk perguruan tinggi tinggi negeri.

Jangan Lupa Untuk Berbagi 🙏Share is Caring 👀 dan JADIKAN HARI INI LUAR BIASA! - WITH GOD ALL THINGS ARE POSSIBLE😊

Mengerjakan pembagian pecahan umumnya kita harus kembalikan ke perkalian pecahan, lihat pada video ini dikerjakan dengan cara pilar (pintar bernalar);

Sumber http://www.defantri.com